Abstract
    A closed loop control system has been designed and built to precisely measure the frequency of a struck piano string.  The sound of the struck string is sampled, filtered, and stored in RAM of a commercial Digital Signal Processor (DSP) chip.  The acquired time-based data is transformed via FFT, and the magnitude squared of frequency spectrum is analyzed.  By using a simple but effective method of interpolating between the two highest points in the power spectrum of the FFT, a frequency measurement of sufficient accuracy is obtained.  The measured frequency is transferred to a supervisory control program where it is compared with a set point frequency.  The error is translated into steps for a stepper motor; the output of the motor is connected to the tuning pin of a piano.  The stepper motor executes the commanded number of steps, and the above process is repeated until the error is tolerably small.  Set point frequencies above and below the middle octave of the piano are determined by measuring or referencing measured second harmonics of the vibrating piano string.

Introduction
    All pianos start going out of tune as soon as the tuning procedure is stopped.  Even if a piano is not played, fluctuations in temperature and humidity combined with about 7 tons of stress in the 200 piano wires causes the individual wires and their respective threaded tuning pins to move and/or change tension.  All pianos, therefore, need tuning - constantly!

    For over 100 years, various devices have been invented for precisely turning a piano tuning pin, but the tool of choice is still the piano tuner's "hammer", essentially a fancy socket wrench with a nice wood handle.  And, since the advent of electronic products, various devices have been invented for precisely measuring the frequency, or at least indicating magnitude of deviation from a desired pitch.

    The device on which this paper is based does both of the above:  it measures frequency and it turns a piano tuning pin.  Since the audience for this paper is composed of DSP technophiles, the emphasis will be on DSP issues.  Only brief mention will be made of other aspects (e.g. mechanical) of the device.

Some piano basics
    A standard piano has 88 keys and about 200 strings.  The upper 68 notes have 3 strings per note while the lower 20 have two or one string per note.  A piano is most noticeably out of tune when the 3 strings of one note are not tuned to the same pitch (or very close).  When two strings are near the same pitch (frequency), but not near enough to be satisfyingly tuned, the difference frequency can be heard as "beats".  The reciprocal of the difference is the period of the beat; e.g. two vibrating strings which are 3 Hz different produce a beat with a period of 1/3 seconds.  Beat periods longer than 3 to 6 seconds (shorter for high notes) are not noticeable because the sound of the struck note has decayed.  Piano note string "unisons" must, therefore, be kept tuned within about 1/6th Hz (in the midrange).

Inharmonicity
    Musical instruments have unique combinations of harmonics which give that instrument its personality or timbre.  The second harmonic of a piano string is produced by each half of a vibrating string, and inharmonicity results because second harmonic frequencies are slightly more than twice the fundamental - the vibrating frequency of the whole string.  This phenomenon is due to the difference in ratio of string (wire) diameter to string length.  The shorter the string relative to its diameter, the stiffer it is.  Evidence of inharmonicity will be provided later.  Other harmonics are subject to the same phenomenon, but this paper is concerned only with the second harmonic.  (Piano tuners use the term "partial".  The first partial is the fundamental; the second partial is the second harmonic, or first overtone, etc.)

CCPPT and the Tuning Procedure
    Figure 1 shows an overview of the Computer Controlled Precision Piano Tuner (CCPPT).  The stepper motor/gear-reducer/socket assembly is suspended (flexibly) over the tuning pin area of a grand piano.  To tune a string, the socket is seated on the desired tuning pin.  The middle octave must be tuned first.  In this implementation, the 12 notes, starting with middle C up to the B above, are tuned to fixed frequencies.  After setting the temperament in this manner, the tuning is unique to each piano because each piano has unique inharmonicity.  All octaves up and down from the middle octave are tuned with reference to the inharmonicity of the second harmonic.  For example, after A-440 is tuned, its second harmonic is recorded; let's say it is 883.4 Hz.   When the A an octave above is tuned, the target (or set point) frequency is 883.4 Hz, not 880 Hz.  See Figure 2.  If a piano is tuned to theoretically calculated frequencies, it would sound flat in the upper register. 
  It should be noted that an expert piano technician does not use the above procedure for setting temperament.  Rather, one note, usually middle A, is tuned to a standard pitch of 440 Hz, and all other notes are tuned relative to this note.  (However, the procedure presented here is pretty good!)

   Again referring to Figure 1, various sub-functions of the CCPPT are:

    1.  User interface
    2.  Data acquisition
    3.  DSP - filtering, FFT, and spectral analysis
    4.  Frequency calculation
    5.  Error calculation and response
    6.  System stress/strain monitoring
    7.  Stepper motor control
 

Data Acquisition
    An electret condenser microphone picks up the piano sounds and connects to an analog-to-digital board containing a 16-bit A/D chip.  The microphone signal is amplified and anti-aliased filtered before its input to the A/D chip.  Potentiometers are used to control signal amplitude such that full A/D range is used without clipping.  Sampling frequency is about 12 KHz which is comfortably more than twice the highest frequency of interest - about 4200 Hz.  The 16-bit sample word is clocked serially from the A/D chip into a serial port on the DSP chip.  The 16-bit fixed point word is easily converted by software into the 32-bit floating point format used by the NEC DSP chip (µPD77230).

µPD77230 DSP
    Figure 3 shows an overview flow chart of the various functions in the DSP program.  The chip has three types of memory on chip:  2K words of instruction ROM, 1K of data ROM, and 2 blocks of data RAM, each 512 words.  All words are 32-bits wide.  In addition, the chip can access external memory containing  instructions, data, or both.  The two ROM areas of this chip (mPD77230-003) are preprogrammed with many standard DSP functions.  The user program for this application executes in external memory and calls the library subroutines in the Instruction ROM.  Library subroutines used in this application include data I/O, RAM initialization, floating point division and square root, an FIR filter subroutine, and 512-point FFT (Fast Fourier Transform).  In order to achieve fast execution, filter coefficients are located in RAM0 while the acquired data is stored in RAM1 (512 words each).
    The external memory on the EB77230 board is shared by the DSP chip and the PC, but only one can access it at a time.  When the user selects a note to be tuned, the PC supervisor program downloads appropriate instruction code and filter coefficients to the shared memory.  On command, the supervisor relinquishes control of memory and releases the DSP chip from reset - thereby  beginning a data acquisition and frequency measurement sequence.  After initialization, the program waits for the piano note to be struck.  When a level is exceeded (note struck), the program waits for about 400 milliseconds before collecting data samples.  The initial percussive effects, therefore, are not sampled.
    In addition to the shared memory, the EB77230 board has two 8-bit latches, each addressed as the same memory location.  One latch signals from DSP to PC; the other, PC to DSP.  The latches operate regardless of  who has control of the shared memory.   Therefore, handshake signals can flow either way at any time.

Figure 4a.  DISPRO Filter Parameter Selection and Comparison Window

Figure 4c.  DISPRO Display of Frequency Response of Example of Lowpass Filter

Figure 4a illustrates how you can tweak the filter parameters to get desired properties.  For example, if you specify a sharper cutoff (transition from pass to stop band), the length of the Parks-McClellan-Remez (PMR) FIR filter gets longer - for a fixed sample rate.  In this example, the cutoff and other parameters were tweaked in order to get the 511 taps.  Filter length must be odd numbered.  Any unused taps in the coefficient file generated from DISPRO are zero filled.  For example, if a 345-tap filter is designed, the 512-345=167 remaining taps are zero filled.  The performance of the filter is unaffected by zero filling unused taps.
    When you accept the design parameters (shown in Fig. 4b.), DISPRO goes to work and performs an iterative procedure involving millions of calculations. Iterations continue until the output response is satisfied.  (A math coprocessor definitely helps!)  Figure 4c is the frequency response plot for the specified filter.
    The appended paper on FFT bin interpolation states that a bandpass filter should be used to pass only the frequency of interest.  For example, even the fundamental should be filtered out when measuring the second harmonic.  Experiments to-date, however, show no difference in measured frequencies when using a lowpass versus a bandpass filter.  Apparently the energies of the two frequencies (fundamental and second harmonic) are far enough apart so as not to affect one another.  Lowpass filters cover a broader range than bandpass, so fewer filters need be used.

Spectral analysis and FFT bin interpolation
    After sample data are acquired, filtered, and stored in RAM, the DSP program performs an FFT and summation of the magnitude squared of real and imaginary data.  All imaginary data is zero filled.  The program then searches this summed data for the two adjoining bins (RAM locations) with the highest values.  Where to search in RAM is specified by parameters downloaded from the PC supervisor.
     Appended to this paper is another paper, FFT Bin Interpolation, written by a good friend and former DSP colleague at NEC, Barry Kulp.  The conclusion from the paper is that, by interpolating between the two highest adjoining values, the peak of the sin(x)/x curve can be determined.  The peak is the frequency of the piano note, either its fundamental or second harmonic.  The appended paper should be studied before proceeding further with this discussion.

Down Sampling
    Down sampling is a means of increasing the resolution of the frequency spectrum.  With a sampling frequency  of 11,894 Hz, together with down sampling, the frequency spacing between bins of a 512 point FFT is as follows:

           R_d             f_t
         Down        FFT          Approx.
       Sampling   Samp         Cutoff            f_bin 
          Rate         Freq*          Freq          Hz per bin ------------------------------------------
       1    11894.0    5500    23.230469
       2     5947.0    2800    11.615234
       3     3964.7    1970     7.743490
       4     2973.5    1450     5.807617
       5     2378.5    1150     4.646094
       6     1982.3     970     3.871745
       7     1699.1     825     3.318638
       8     1486.8     720     2.903809
       9     1321.6     640     2.581163
      10     1189.4     570     2.323047     ------------------------------------------
      20      594.7     280     1.161523
 -----------------------------------------
      54      220.4     110     0.430194

             * also referred to as the "Fourier frequency" 

Figure 5.  FFT Bin Interpolation

        Magnitude Squared Power Spectrum When Measuring Frequency of Middle C

 

Terms defined: Peak is the peak of the sinx/x shaped curved connecting the points of the power spectrum.  First, find the highest two adjoining values in the magnitude squared power spectrum.  The peak is usually between two points (or bins) of an FFT.  Usually one bin's value is higher than the other.  However, if two adjacent bins have the same value, the peak lies exactly between the two bin numbers.  In the other unlikely extreme, if the values on either side of the highest value are equal, then the highest value is the peak of the superimposed sinx/x curve. L = square root of value in the lower location of the two bins; (lower of the two adjoining highest values). H = square root of value in the higher location of the two bins  B = bin # of L D  = H/(L + H) = a fraction of fbin (see below) This is the distance from lower bin # to peak. fsamp = Sampling frequency Rd = down sampling rate "Fourier frequency" = fsamp/Rd fbin = frequency increment from one FFT bin to the next higher fbin = Fourier frequency/FFT size fpeak = Frequency at peak = (B + D ) • (fbin)

Example calculation using Middle C measurements: FFT size = 512 points Fsamp = 11,894 Hz,       Rd = 11 Fundamental: L =  (2116.94)1/2=46.0102 H = (4101.10)1/2 = 64.0398 D  = H/(L + H) = 0.5819155 B = 123 fbin = (11,894/11) / 512  = 2.11186 Hz fpeak = (123 + 0.582)   2.112 = 260.988 Hz Second Harmonic: L =  (3020.44)1/2 = 54.9585 H = (402.256)1/2 = 20.0563  D  = H/(L + H) = 0.267365 B = 249 fpeak = (249.267) • 2.112 = 526.418 Hz   Note that twice the fundamental is       2 • 260.988 = 521.976 Hz Due to inharmonicity, therefore, the actual second harmonic is 526.42 - 522.0 = 4.44 Hz higher than the theoretical second harmonic.  This inharmonicity is the key factor in tuning a piano correctly.

Frequency calculation
    Figure 5 shows an example of the frequency calculation using real world data from middle C on a piano.  The topmost plot of RAM data (spectrum) shows the symmetry of the lower 256 points with the upper 256.  As mentioned earlier, the supervisor program accesses table data consisting of previously calculated parameters pertaining to the note being tuned.  For tuning middle C, the supervisor would write to the memory shared by the DSP program a down sample rate of 11; further, it would tell where to start looking in RAM for the fundamental and how many bins to search.  Another parameter would tell where to look for the second harmonic.
    From the human user's point of view, the display of the calculated frequency is almost instantaneous after striking the piano key.  Some of the delay, of course, is intentional - in order to disregard the initial percussive effects.    As you might expect, the harder the piano key is struck, the bigger the numbers in the power spectrum.   It is interesting to note also that, because the sound is sampled at a fixed time delay after the key is struck, the frequency measured is higher for a hard hit key than for a softer strike.  The greater amplitude of the vibrating string makes the string more taut during the brief time that the sound is being sampled.  This condition suggests the use of a controlled blow for consistent precise measurements.
    (Striking the key with a good blow is important for getting equal tension in all portions of the taut wire, e.g. on either side of the bridge.)
    The subject of inharmonicity appears throughout piano tuning literature.  Observe in Figure 5 that inharmonicity, in the measurement of middle C on the baby grand piano used for this experiment, comes through "loud and clear".  (A large grand piano has less inharmonicity because the strings are longer relative to diameter.)

Error calculation and response
    This being a closed loop control system, the supervisor must evaluate the sensor input (measured frequency), compare the value with a set point (target frequency), calculate a response, and send commands to adjust the system (or plant) so as to reduce the error.
    Consider the case where a measured frequency is sharp compared with the target frequency.  As presently implemented, the system will start all over in order to tune the note.  That is, the tuning pin will be turned so as to flatten the note below the target, and then approach the target asymptotically from below. This, then, is an over-damped control system where it is important not to overshoot the target.  Piano tuners usually work the other way; that is, they tune a note slightly sharp and then back off slightly.  Experience may indicate that the CCPPT should use the same procedure.  If so, a small software change in the supervisor program is required.
    Data was obtained in manual mode in order to derive steps-per-hertz response.  In the vicinity of middle C, frequencies were recorded after 50-step increments.  A plot of the data shows a pretty linear response of about 87 steps per hertz.
    In our example, where the note measures 260.988 Hz, the calculated response is 87 x (261.626 - 260.638) or 55 steps in the sharp direction.  Since it is important not to overshoot, something less 55 steps will commanded to the stepper motor.  The process of measuring and responding is repeated until the error is tolerably small.  In this region of the piano, 0.638 Hz error is not acceptable.  A beat period of 1/0.638 (about 1.5 seconds) is readily detected.
    Piano tuners use the term "cents" to describe the amount of error.  A "cent" is 1/100th of a 1/2 step interval.  In this case, the half-step interval from C-4 to C#-4 is 15.6 Hz, so one cent is 0.156 Hz.  Our Fig. 5 example note is about 4 cents flat.  Table data is also referenced by the Supervisor to judge when the error is below a maximum value.  When this point is reached, the note is tuned.  Arbitrarily, the maximum error is set at one Cent.

Non-linear response
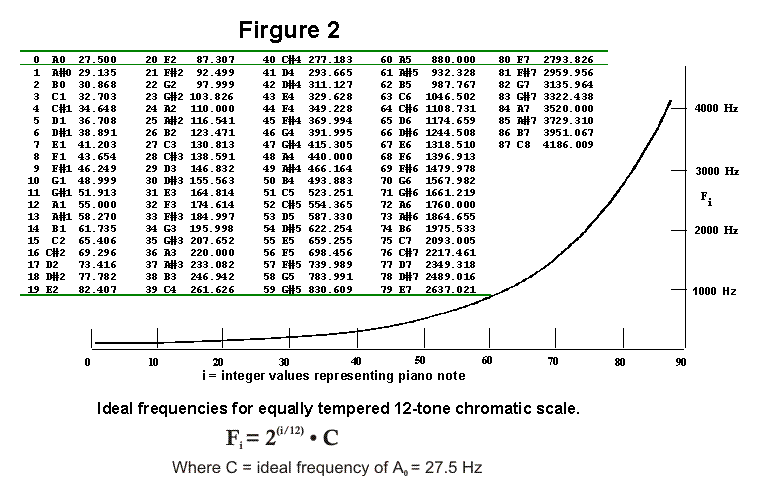
    As seen in Figure 2, the half step interval from C1 to C#1 is only about 1.9 Hz, whereas from C7 to C#7, the difference is about 124 Hz.  In the first example, one cent is 0.019 Hz; in the second example, 1.24 Hz.  The response calculation must account for this non-linearity.  Steps-per-Hertz data was derived experimentally from various regions of the piano, and a curve fitted to the compiled data.  The curve looks like the mirror image of Figure 2.  For example, for the lowest notes, about 1600 steps are required to raise the frequency by one Hertz, whereas near the top, only 4 steps are required.  The change in Steps-per-Cent is much less:  about 40 Steps/Cent for low notes, about 7 Steps/Cent for high notes.
    High notes fade much faster than low notes, so beats are much harder to hear.  High notes, then, are more difficult to tune manually than low notes.  CCPPT doesn't care which region is being tuned because the algorithm is not concerned with beats.
    Different size pianos have different length strings.  The bigger the piano, the higher the number of Steps-per-Hertz.  The referenced look-up table data is just a starting point.  After the system is fully tensioned (see next section), the Supervisor can gather its own Steps-per-Hertz data for the particular piano being tuned.  The response calculation is adjusted accordingly.

System stress/strain monitoring
    Up to this point, mechanical issues have not been discussed.  But they can't be ignored!  Starting with a slip-fitting socket that engages the tuning pin, through gearing and motor, and on through linkage in the torque restraining bar to the clamp secured to the piano frame (see Figure 1), there are many sources of backlash.  The system supervisor, therefore, needs to know when the motor is stepping against a torque load or is just turning to take up mechanical slop in the system.  In order to monitor system strain, two strain gages are mounted on flat spots in the middle of the torque restrainer bar.  The electrical resistance of a strain gage varies with strain.  The two strain gages in the CCPPT form the variable resistances in a bridge circuit.  The voltage output from the circuit is amplified and input to an 8-bit A/D converter which is incorporated in the micro-controller chip (µPD7811) which controls the stepper motor.  (This A/D converter has nothing to do with the A/D converter for the audio signal.)  The A/D reading is passed back to the supervisor as part of its routine data exchange when a move has been completed.  One of the coded commands from the PC to the motor controller is simply:  step in the sharp direction until the strain gage reading = x value.  In order to aid the tuning process while in Manual mode, the strain gage reading is converted to one of eight levels, and the resulting value is output to 8 LEDs.  One of two additional LEDs indicates the direction of the strain.  The vector is also displayed on the PC screen.

Stepper motor control
    When the commanded number of steps is received by the µPD7811 from the PC supervisor, the number is read by a timer interrupt service as a counter.  The interrupt service increments or decrements (depending on commanded direction) through a table of stepper motor output patterns.  Four wires connect to poles in the stepper motor; a pattern consists of some pair being turned on while the other pair is off.  The counter is decremented with each change in output pattern - until the counter is zero; job done.

Piano tuner's skepticism
    When demonstrating the CCPPT at a Piano Technicians Guild convention (April 1992), the most common observation/criticism by the professionals focused on the actual turning of the tuning pin.  Many tuners feel that manipulating the "hammer" (wrench) is the real art in tuning a piano so that it stays tuned.  (No piano does, but it's all relative!)  Only experience will vindicate or dispel the professional tuner's skepticism.  However, tuners are likely to underestimate the power,  flexibility, and repeatability of digital control!
    One action which the CCPPT does not do but which human tuners cannot help doing is bending the tuning pin; not literally bending it, but leaning perpendicular to the axis of the pin in order to back off ever so slightly.  Over a period of many tunings, bending the pin will cause it to loosen in the wooden pin block.

Improving precision in frequency measurement
    In selecting components for the CCPPT prototype, high precision was a priority.  There are, however, a number of steps which can yield still more precision if experience indicates a need.  A 16-bit A/D converter is quite standard, but more precise (e.g. 18-bit)  converters than the one used here are available.  As for FFT's, every doubling in size reduces the distance between bins by half.  NEC has just published an 8K-point FFT application note.  This is 16 times bigger than the 512-point FFT used here.  Using the 8K FFT, the interpolation process, then, would be 16 times more precise.  If the 8K FFT calculation were deemed too slow (it is much less than 1 second), then a faster DSP chip is available from NEC (µPD77240).
    A higher sampling frequency would allow more precise down sampling, particularly for measuring the high notes.  The "Fourier frequency" (see Appendix) could then be closer to exactly four times the frequency of interest.
    As mentioned above, the algorithm used here does not use beats for setting temperament; that is, setting the intervals in the middle octave.  If such a procedure were desired, then frequencies of harmonics other than second harmonic could be measured, stored, and referenced for calculating a beat frequency of interest - for example in setting the major sixth or major third intervals, e.g. C4 to A4 or C4 to E4 respectively.  (No interval is beatless in a 12-tone tempered scale.)

Conclusion
    Digital Signal Processing opens the door for economical and precise analysis and measurement of piano sounds.  A closed-loop digital servo loop using an electric motor provides a method of turning the piano's tuning pins in a precise repeatable manner.

Click to view picture taken at Piano Technicians Guild Regional Seminar.

Click to view a later revision to the hardware implementation.

Click to view a video of a hand operated version.  No motor used.

               Acknowledgments: